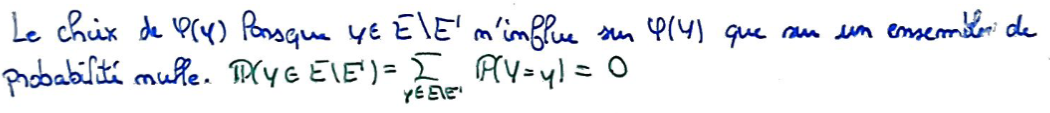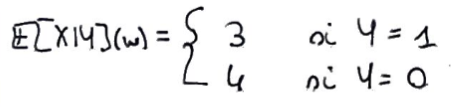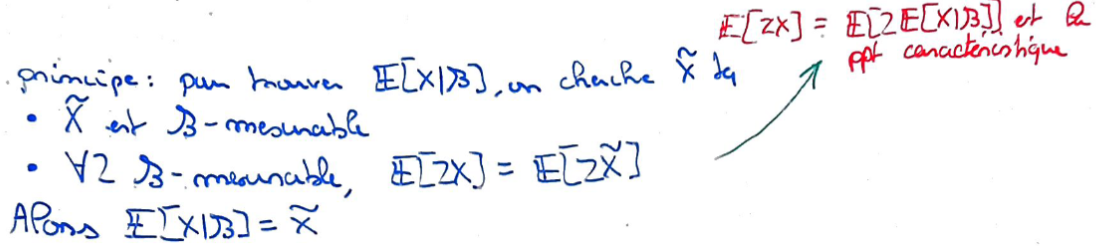Math'φsics

Menu
  • Acceuil
  • Maths
  • Physique
    • Maths
    • Physique
  • Espérance conditionnelle

    Formulaire de report


    Selon un événement

    Espérance conditionnelle \({\Bbb E}[X|B]\) selon l'événement \(B\)
    Valeur donnée par : $${\Bbb E}[X|B]:=\frac{{\Bbb E}[X\Bbb 1_B]}{{\Bbb P}(B)}$$
    • bien définie lorsque \(X\in L^1\)


    Selon une v.a. Discrète

    Espérance conditionnelle \({\Bbb E}[X|Y]\) selon une v.a. Discrète \(Y\)
    Variable aléatoire définie par : $${\Bbb E}[X|Y]=\varphi(Y)\quad\text{ avec }\quad \varphi:y\mapsto\begin{cases}{\Bbb E}[X|Y=y]&\text{si}\quad y\in E^\prime\\ 0&\text{sinon.}&\end{cases}$$ avec \(E^\prime=\{y\in E\mid {\Bbb P}(Y=y)\gt 0\}\).
    • interprétation : il s'agit de la moyenne de \(X\) lorsqu'on connaît \(Y\)
    • \({\Bbb E}[\lvert{\Bbb E}[X|Y]\rvert]\leqslant\) \({\Bbb E}[\lvert X\rvert]\)
    • propriété caractéristique : pour toute v.a. Réelle \(Z\) \(\sigma(Y)\)-mesurable, $${\Bbb E}[Z{\Bbb E}[X|Y]]={\Bbb E}[ZX]$$


    Questions de cours

    START
    Ω Basique (+inversé optionnel)
    Recto: Expliquer en quoi le choix de la valeur \(\varphi(y)\) lorsque \(y\in E\setminus E^\prime\) a peu d'importance.
    Verso: Car c'est un ensemble de probabilité nulle.

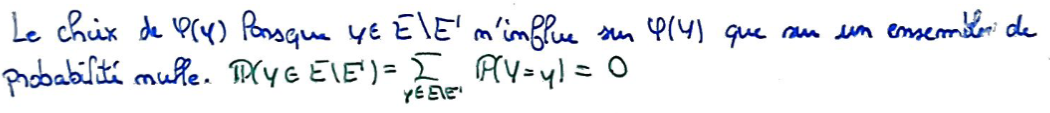
    Bonus:
    Carte inversée ?:
    END
    START
    Ω Basique (+inversé optionnel)
    Recto: Calculer \({\Bbb E}[X|Y]\).

    Verso:

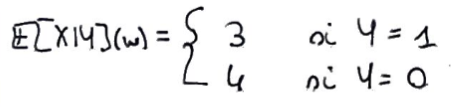
    Bonus:
    Carte inversée ?:
    END
    Montrer que si \(Y\) est discrète, alors

    Partir de la définition.

    Majorer en sachant qu'il y a toujours exactement un terme non nul dans la somme.


    Montrer que si \(Y\) est une v.a. Discrète, pour toute v.a. Réelle \(Z\) \(\sigma(Y)\)-mesurable, $${\Bbb E}[Z{\Bbb E}[X|Y]]={\Bbb E}[ZX]$$

    Puisque \(Z\) est \(\sigma(Y)\)-mesurable, on a \(Z=f(Y)\) avec \(f\) bornée.

    Réécrire la définition en sachant cela.

    Bouger l'espérance et enlever la somme superflue.


    Montrer que pour une v.a. Discrète, \({\Bbb E}[X|Y]\) ne dépend que de \(\sigma(Y)\).

    Pour tout autre v.a. Discrète qui engendre la même tribu, on a aussi la propriété caractéristique.

    On pose en particulier \(Z\) l'indicatrice qui indique lorsqu'une espérance conditionnelle est supérieure à une autre.

    En soustrayant les deux propriétés caractéristiques, on a que cette indicatrice est nulle.

    Par symétrie, les deux sont égales.



    Selon une sous-tribu/v.a. Continue

    Espérance conditionnelle \({\Bbb E}[X|{\mathcal B}]\) selon une sous-tribu \({\mathcal B}\)
    Variable aléatoire \(\underline {\mathcal B}\)-mesurable qui respecte la propriété caractéristique : $$\forall B\in{\mathcal B},\quad{\Bbb E}[\Bbb1_B{\Bbb E}[X|{\mathcal B}]]={\Bbb E}[\Bbb 1_BX]$$
    • la propriété caractéristique peut être étendue aux v.a. \({\mathcal B}\)-mesurables et bornées : \({\Bbb E}[ZX]={\Bbb E}[Z{\Bbb E}[X|{\mathcal B}]]\)
    • on a existence et unicité pour \(X\) intégrable ou à valeur dans \([0,+\infty]\)
    • en particulier, on note \({\Bbb E}[X|Y]:=\) \({\Bbb E}[X|\sigma(Y)]\)
    • si \(X\) est \({\mathcal B}\)-mesurable, alors \({\Bbb E}[X|{\mathcal B}]=X\) (conditionner par \({\mathcal B}\) ne donne pas d'infos supplémentaires)
    • espérance : \({\Bbb E}[{\Bbb E}[X|{\mathcal B}]]=\) \({\Bbb E}[X]\)
    • \(\lvert{\Bbb E}[X|{\mathcal B}]\rvert\leqslant\) \({\Bbb E}[\lvert X\rvert|{\mathcal B}]\)
    • \({\Bbb E}[\cdot|{\mathcal B}]\) est linéaire et croissante
    • pour \(A\in\mathcal A\), on note \({\Bbb P}(A|{\mathcal B})=\) \({\Bbb E}[\Bbb 1_A|{\mathcal B}]\)
    • pour \(X\in L^2\), coïncide avec la Projection orthogonale de \(X\) sur \(L^2(\Omega,{\mathcal B},{\Bbb P})\)
      •     
    • en particulier, $$\lVert X-{\Bbb E}[X|{\mathcal B}]\rVert_2=\inf_{Z\in L^2(\Omega,{\mathcal B},{\Bbb P})}\lVert X-Z\rVert_2$$
    • si \(Y\) est \({\mathcal B}\)-mesurable, alors \({\Bbb E}[XY|{\mathcal B}]=\) \(Y{\Bbb E}[X|{\mathcal B}]\)
    • tribus emboîtées : si \({\mathcal B}_1\subset{\mathcal B}_2\), alors \({\Bbb E}[{\Bbb E}[X|{\mathcal B}_2]|{\mathcal B}_1]={\Bbb E}[X|{\mathcal B}_1]\)
    • si \(Y\) est \({\mathcal B}\)-mesurable, \(X\) est indépendante de \({\mathcal B}\) et \(g:E\times E^\prime\to{\Bbb R}_+\) est mesurable, alors \({\Bbb E}[g(X,Y)|{\mathcal B}]\) est donnée par : \(\int_E g(x,Y){\Bbb P}_X(dx)\)
      •     
    • en particulier, \({\Bbb E}[f(X,Y)|X]\) est donnée par : $${\Bbb E}[f(X,Y)|X]={\Bbb E}[f(\cdot,Y)](X)=\int f(X,y)\,{\Bbb P}_Y(dy)$$
    • si \(\mathcal H_2\) est indépendante de \(\mathcal H_1\lor\sigma(X)\), alors \({\Bbb E}[X|\mathcal H_1\lor\mathcal H_2]=\) \({\Bbb E}[X|\mathcal H_1]\)


    Pour une v.a. Intégrable

    Démontrer que \({\Bbb E}[X|{\mathcal B}]\) est unique pour \(X\) intégrable.

    On suppose qu'il existe deux v.a. Intégrables qui respectent la propriété caractéristique.

    En soustrayant les deux relations, on a une espérance nulle.

    On prend \(B\) indiquant qu'une v.a. Est plus grande que l'autre.

    Puisque l'espérance est nulle, on en déduit que les v.a. Sont ps constantes.


    Démontrer l'existence de \({\Bbb E}[X|{\mathcal B}]\) pour \(X\) intégrable.

    On se restreint au cas positif et d'espérance finie et on pose une mesure qui associe à tout ensemble \(B\) l'espérance du produit de son indicatrice avec \(B\)

    La mesure est absolument continue, donc par le Théorème de Radon-Nikodym, on en déduit l'existence d'une v.a. \(\tilde X\) tq \(Q(B)={\Bbb E}[\Bbb 1_B\tilde X]\).

    C'est vrai \(\forall B\), ce qui nous donne l'existence d'une v.a. Qui vérifie la propriété caractéristique.

    Dans le cas général, on décompose \(X=X^+-X^-\) et on procède par linéarité.

    La deuxième propriété caractéristique s'obtient par linéarité pour les v.a. Étagées, puis par passage à la limite.


    Montrer que $${\Bbb E}[{\Bbb E}[X|{\mathcal B}]]={\Bbb E}[X].$$

    C'est la propriété caractéristique avec \(B=\Omega\).

    Montrer que \({\Bbb E}[\cdot|{\mathcal B}]\) est linéaire.

    On utilise la propriété caractéristique des espérances conditionnelles intermédiaires pour décomposer.

    On vérifie que ce qu'on obtient vérifie la propriété caractéristique de \({\Bbb E}[\lambda X+\lambda^\prime X^\prime|{\mathcal B}]\) pour conclure par unicité.


    Démontrer la propriété suivante :

    Il suffit de décomposer \(X=X^+-X^-\), d'utiliser la linéarité et de conclure par inégalité triangulaire.



    Pour une v.a. Positive

    Démontrer l'existence de \({\Bbb E}[X|{\mathcal B}]\) pour \(X\) positive.

    On le définit à partir de v.a. Bornées (donc intégrables), en utilisant des suites croissantes.

    La deuxième propriété caractéristique se vérifie également à partir du cas intégrable, en prenant \(Z\) limite d'une suite croissante de v.a..


    Démontrer l'unicité de \({\Bbb E}[X|{\mathcal B}]\) pour \(X\) positive.

    On suppose qu'il existe deux v.a. Et on prend pour la propriété caractéristique un événement distant que l'un est plus petit que l'autre (en faisant gaffe aux cas infinis.)

    Cela permet d'encadrer \({\Bbb E}[\Bbb 1_BX^\prime]\) via \({\Bbb P}(B)\), ce qui fait que \({\Bbb P}(B)=0\).

    On peut généraliser à tout \(a,b\) via une union dénombrable, ce qui fait que les deux v.a. Sont ps égales.


    START
    Ω Basique (+inversé optionnel)
    Recto: Ecrire le Théorème de convergence monotone pour des espérances conditionnelles.
    Verso: $$X_n\geqslant0, X_n\uparrow X\implies{\Bbb E}[X_n|{\mathcal B}]\uparrow{\Bbb E}[X|{\mathcal B}]$$
    Bonus:
    Carte inversée ?: y
    END
    START
    Ω Basique (+inversé optionnel)
    Recto: Ecrire le Lemme de Fatou pour des espérances conditionnelles.
    Verso: $${\Bbb E}[\varliminf X_n|{\mathcal B}]\leqslant\varliminf{\Bbb E}[X_n|{\mathcal B}]$$
    Bonus:
    Carte inversée ?: y
    END
    START
    Ω Basique (+inversé optionnel)
    Recto: Ecrire le Théorème de convergence dominée pour des espérances conditionnelles.
    Verso: $$X_n\in{\Bbb R},\lvert X_n\rvert\leqslant Z,{\Bbb E}[Z]\lt +\infty,X_n\to X\implies{\Bbb E}[X_n|{\mathcal B}]\overset{L^1}\longrightarrow{\Bbb E}[X|{\mathcal B}]$$
    Bonus:
    Carte inversée ?: y
    END
    START
    Ω Basique (+inversé optionnel)
    Recto: Ecrire l'Inégalité de Jensen pour des espérances conditionnelles.
    Verso: $$f:{\Bbb R}\to{\Bbb R}_+\text{ convexe},X\in L^1(\Omega,\mathcal A,{\Bbb P})\implies{\Bbb E}[f(X)|{\mathcal B}]\geqslant f({\Bbb E}[X|{\mathcal B}])$$
    Bonus:
    Carte inversée ?: y
    END
    Démontrer le Théorème de convergence monotone de l'espérance conditionnelle pour des v.a. Positives.

    On utilise le TCM sur la propriété caractéristique.


    Démontrer l'Inégalité de Jensen pour l'espérance conditionnelle.

    On utilise un \(\sup\) de fonctions affines et on procède par linéarité de l'espérance.


    START
    Ω Basique (+inversé optionnel)
    Recto: Comment calculer \({\Bbb E}[X|{\mathcal B}]\) en pratique ?
    Verso:

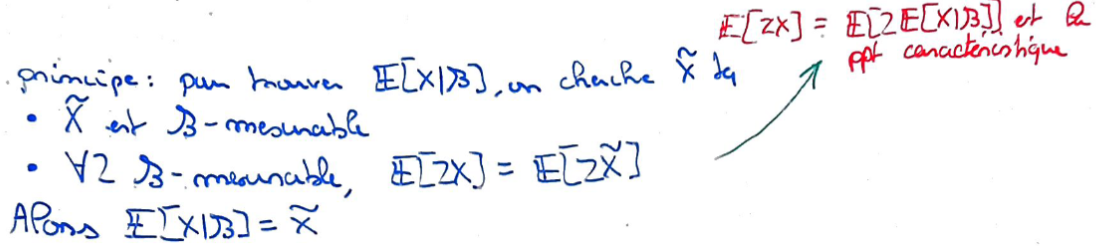
    Bonus:

    Carte inversée ?:
    END
    Montrer que \(X\mapsto{\Bbb E}[X|{\mathcal B}]\) est une contraction de \(L^p\) pour \(p\geqslant1\).

    On utilise l'inégalité de Jensen.


    Démontrer :

    On utilise la caractérisation. \(\in L^2\) ok par majoration du moment.

    Le caractère orthogonal se fait par linéarité de l'espérance conditionnelle.


    Démontrer :

    On peut se restreindre au cas positif et vérifier la proposition caractéristique.


    Démontrer :

    On utilise le fait que \(Z\) est \({\mathcal B}_1\)-mesurable (et donc aussi \({\mathcal B}_2\)-mesurable) pour vérifier la propriété caractéristique.


    Démontrer :

    On veut utiliser la propriété caractéristique \(\to\) on peut séparer la loi par indépendance.

    On utilise Fubini pour séparer l'intégrale et on conclut par propriété caractéristique.


    Démontrer :

    Il suffit de vérifier la propriété caractéristique avec en prenant des éléments quelconques de chaque tribu.

    On sépare l'espérance par indépendance et on replace un côté via la propriété caractéristique.

    On réunit les espérances pour avoir la propriété caractéristique sur l'ensemble.

    On utilise le Lemme de classe monotone pour généraliser le résultat à tout \(\mathcal H_1\lor\mathcal H_2\).


    START
    Ω Basique (+inversé optionnel)
    Recto: Comment s'écrit un élément de la tribu \(\mathcal H_1\lor\mathcal H_2\) ?
    Verso: La tribu est engendrée par la Classe monotone formée des $$B=B_1\cap B_2\quad\text{ avec }\quad B_1\in\mathcal H_1,B_2\in\mathcal H_2.$$
    Bonus:
    Carte inversée ?:
    END

    Calcul d'espérance conditionnelle

    START
    Ω Basique (+inversé optionnel)
    Recto: Comment calculer une espérance conditionnelle dans le cas discret ?
    Verso: $${\Bbb E}[X|Y]=\psi(Y)\quad\text{ avec }\quad \psi:y\mapsto\begin{cases}\displaystyle{\Bbb E}[X|Y=y]=\frac{{\Bbb E}[X\Bbb 1_{\{Y=y\} }]}{{\Bbb P}(Y=y)}&\text{si}\quad{\Bbb P}(Y=y)\gt 0\\ 0&\text{sinon.}&\end{cases}$$
    Bonus:
    Carte inversée ?:
    END
    START
    Ω Basique (+inversé optionnel)
    Recto: Comment calculer une espérance conditionnelle dans le cas à densité ?
    Verso: $${\Bbb E}[g(X)|Y]=\psi_g(Y)\quad\text{ avec }\quad \psi_g:y\mapsto\begin{cases}\displaystyle\frac1{q(y)}\int_{{\Bbb R}^n}g(x)p(x,y)\,dx&\text{si}\quad q(y)\gt 0\\ g(0)&\text{sinon.}&\end{cases}$$ avec \(q\) la loi de \(Y\) donnée par \(q(y)=\int_{{\Bbb R}^m}p(x,y)\,dx\).
    Bonus: On peut écrire $$\psi_g(y)=\int_{{\Bbb R}^n}g(x)\nu(y,dx)\quad\text{ avec }\quad\nu(y,dx)=\begin{cases}\displaystyle\frac{p(x,y)}{q(y)}\,dx&\text{si}\quad q(y)\gt 0\\ \delta_0(dx)&\text{sinon.}&\end{cases}$$ et \(\nu(y,dx)\) est la Loi conditionnelle de \(X\) sachant \(Y=y\).
    Carte inversée ?:
    END
    Démontrer :

    On utilise la formule de transfert pour essayer d'avoir la propriété caractéristique.

    On sépare l'intégrale par Fubini et on reconnaît \(\psi_g\) et les lois.



    Calculer la densité de \((X,Y)\) via un changement de variables.

    Intégrer cette densité selon \(x\).

    En déduire la loi conditionnelle via la formule.



    Exercices


    On pose \(g:x\mapsto{\Bbb E}[f(x,Y)]\) \(\to\) elle est mesurable d'après le Théorème de Fubini-Tonelli, ce qui fait que \(g(X)\) est une v.a. \(\sigma(X)\)-mesurable

    Il suffit alors de passer par la propriété caractéristique.

    On prend une variable \(\sigma(X)\)-mesurable, qu'on écrit sous la forme \(h(X)\) avec \(h\) bornée mesurable.

    On écrit \({\Bbb E}[h(X)g(X)]\) sous forme intégrale via le Théorème de transfert et on développe \(g\).

    On peut utiliser le Théorème de Fubini-Tonelli pour passer aux mesures produits, ce qui nous donne le résultat.



    Par indépendance, on peut utiliser la formule de la question précédente.

    On écrit l'espérance sous forme intégrale.

    L'intégrale peu être calculée en séparant la fraction.

    En changeant \(y\) par \(Y\), on obtient le résultat.



    L'égalité est satisfaite car \(\mathcal C\subset{\mathcal F}\).

    Démontrer l'unicité revient à démontrer que, si une autre v.a. Satisfait l'égalité, alors ces deux variables sont égales \(\forall A\in{\mathcal F}\), ce qui permettra de conclure par unicité de l'espérance conditionnelle.

    On pose l'ensemble des \(A\in{\mathcal F}\) pour lesquels on a l'égalité.

    On vérifie que c'est une Classe monotone.

    On conclut via le Lemme de classe monotone, puisque \(\mathcal C\subset\mathcal D\), et \(\mathcal C\) est stable par intersection finie.



    On définit une classe stable par intersection finie qui engendre \({\mathcal B}_1\lor{\mathcal B}_2\).

    On veut vérifier la propriété caractéristique sur les éléments de \(\mathcal C\), ce qui est facilité par le fait qu'ils s'écrivent comme une intersection.

    On peut séparer l'espérance par indépendance.

    On utilise la propriété caractéristique de \({\Bbb E}[Y|{\mathcal B}_1]\) pour faire apparaître l'espérance conditionnelle.

    On peut alors faire revenir \(\Bbb 1_{B_2}\) et réunir les indicatrices.

    La propriété caractéristique est vérifiée sur un ensemble stable par intersections finies qui engendre \({\mathcal B}_1\lor{\mathcal B}_2\), ce qui permet de conclure.


    START
    Ω Basique (+inversé optionnel)
    Recto: Qu'est-ce que \({\Bbb P}(X\geqslant t|{\mathcal F})\) ?
    Verso: C'est l'espérance conditionnelle $${\Bbb E}[\Bbb 1_{X\geqslant t}|{\mathcal F}]$$
    Bonus:
    Carte inversée ?: y
    END

    On utilise la positivité et la linéarité de l'intégrale conditionnelle pour majorer \({\Bbb P}(X\geqslant t|{\mathcal F})\), de la même manière que dans la démonstration de l'Inégalité de Markov.

    On obtient le résultat voulu par positivité, en majorant l'indicatrice.


  • Rétroliens :
    • Famille de tribus indépendantes
    • Loi conditionnelle
    • Loi forte des grands nombres
    • Martingale
    • Uniforme intégrabilité
    • Variables aléatoires indépendantes